Sean dos vectores  y
y  en el espacio vectorial
en el espacio vectorial  . El producto vectorial entre
. El producto vectorial entre  y
y  da como resultado un nuevo vector,
da como resultado un nuevo vector,  . Para definir este nuevo vector es necesario especificar su módulo y dirección:
. Para definir este nuevo vector es necesario especificar su módulo y dirección:
 y
y  en el espacio vectorial
en el espacio vectorial  . El producto vectorial entre
. El producto vectorial entre  y
y  da como resultado un nuevo vector,
da como resultado un nuevo vector,  . Para definir este nuevo vector es necesario especificar su módulo y dirección:
. Para definir este nuevo vector es necesario especificar su módulo y dirección:- El módulo de
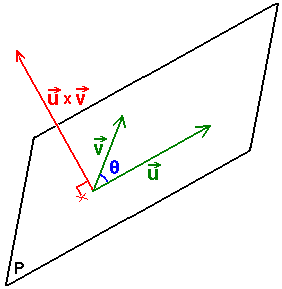
 está dado por
está dado por
donde θ es el ángulo determinado por los vectores a y b.
- La dirección del vector c, que es ortogonal a a y ortogonal a b, está dada por la regla de la mano derecha.
El producto vectorial entre a y b se denota mediante a × b, por ello se lo llama también producto cruz. En los textos manuscritos, para evitar confusiones con la letra x (equis), es frecuente denotar el producto vectorial mediante a ∧ b.
El producto vectorial puede definirse de una manera más compacta de la siguiente manera:
donde  es el vector unitario y ortogonal a los vectores a y b y su dirección está dada por la regla de la mano derecha y θ es, como antes, el ángulo entre a y b. A la regla de la mano derecha se la llama a menudo también regla del sacacorcho.
es el vector unitario y ortogonal a los vectores a y b y su dirección está dada por la regla de la mano derecha y θ es, como antes, el ángulo entre a y b. A la regla de la mano derecha se la llama a menudo también regla del sacacorcho.
 es el vector unitario y ortogonal a los vectores a y b y su dirección está dada por la regla de la mano derecha y θ es, como antes, el ángulo entre a y b. A la regla de la mano derecha se la llama a menudo también regla del sacacorcho.
es el vector unitario y ortogonal a los vectores a y b y su dirección está dada por la regla de la mano derecha y θ es, como antes, el ángulo entre a y b. A la regla de la mano derecha se la llama a menudo también regla del sacacorcho.Producto vectorial de dos vectores
Se define el producto  , y se escribe
, y se escribe  , como el vector:
, como el vector:
 , y se escribe
, y se escribe  , como el vector:
, como el vector:En el que
 , es el determinante de orden 2.
, es el determinante de orden 2.
O usando una notación más compacta, mediante el desarrollo por la primera fila de un determinante simbólico de orden 3 (simbólico ya que los términos de la primera fila no son escalares):
Que da origen a la llamada regla de la mano derecha o regla del sacacorchos: girando el primer vector hacia el segundo por el ángulo más pequeño, la dirección de  es el de un sacacorchos que gire en la misma dirección.
es el de un sacacorchos que gire en la misma dirección.
 es el de un sacacorchos que gire en la misma dirección.
es el de un sacacorchos que gire en la misma dirección.La siguiente expresión, aunque carece de significado matemático estricto, sirve de método nemónico para recordar el orden de las coordenadas en el producto:[cita requerida]
Ejemplo
El producto vectorial de los vectores  y
y  se calcula del siguiente modo:
se calcula del siguiente modo:
 y
y  se calcula del siguiente modo:
se calcula del siguiente modo:Expandiendo el determinante:
Puede verificarse fácilmente que  es ortogonal a los vectores
es ortogonal a los vectores  y
y  efectuando el producto escalar y verificando que éste es nulo (condición de perpendicularidad de vectores).
efectuando el producto escalar y verificando que éste es nulo (condición de perpendicularidad de vectores).
Texto de lectura recomendado: Una epistemologia historica del producto vectorial
 es ortogonal a los vectores
es ortogonal a los vectores  y
y  efectuando el producto escalar y verificando que éste es nulo (condición de perpendicularidad de vectores).
efectuando el producto escalar y verificando que éste es nulo (condición de perpendicularidad de vectores).Latin-American Journal of Physics Education
Texto de lectura recomendado: Una epistemologia historica del producto vectorial
Fuente: wikipedia



 y
y  dos vectores concurrentes de
dos vectores concurrentes de 





No hay comentarios:
Publicar un comentario