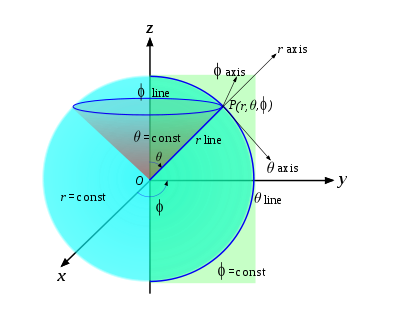
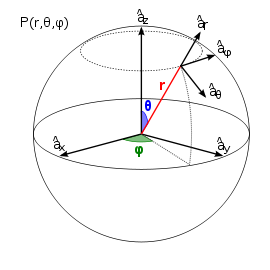
Coordenadas esféricas
El sistema de coordenadas esféricas se basa en la misma idea que las coordenadas polares y se utiliza para determinar
la posición espacial de un punto mediante una distancia y dos ángulos.
En consecuencia, un punto P queda representado por un conjunto de tres magnitudes: el radio  , el ángulo polar
, el ángulo polar
 , el ángulo polar
, el ángulo polarAlgunos autores utilizan la latitud, en lugar de colatitud, en cuyo caso su margen es de 90º a -90º
(de -π/2 a π/2radianes), siendo el cero el plano XY. También puede variar la medida del acimut, según se mida
el ángulo en sentido reloj o contrarreloj, y de 0º a 360º (0 a 2π en radianes) o de -180º a +180º (-π a π).
Se debe tener en cuenta qué convención utiliza un autor determinado.
Convenciones utilizadas
Convención estadounidense
Actualmente, el convenio usado en los EEUU es el mismo que el europeo. Para denotar el ángulo azimutal
se usa φ y para referirse al polar, latitud o colatitud se usa θ.
Convención no-estadounidense
Sin embargo, la mayoría de los físicos, ingenieros y matemáticos no norteamericanos intercambian los símbolos θ y φ, siendo:
- θ la colatitud, de 0º a 180º
- φ el azimuth, de 0º a 360º
Esta es la convención que se sigue en este artículo. En el sistema internacional, los rangos de variación de las tres
coordenadas son:
La coordenada radial es siempre positiva. Si reduciendo el valor de  llega a alcanzarse el valor 0, a partir de ahí,
llega a alcanzarse el valor 0, a partir de ahí,
 llega a alcanzarse el valor 0, a partir de ahí,
llega a alcanzarse el valor 0, a partir de ahí, ; vuelve a aumentar, pero θ pasa a valer π-θ y φ aumenta o disminuye en π radianes.
; vuelve a aumentar, pero θ pasa a valer π-θ y φ aumenta o disminuye en π radianes.
Relación con otros sistemas de coordenadas
Relación con las coordenadas cartesianas
Sobre los conjuntos abiertos:
Existe una correspondencia unívoca 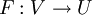 entre las coordenadas cartesianas y las esféricas, definidas
entre las coordenadas cartesianas y las esféricas, definidas
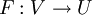 entre las coordenadas cartesianas y las esféricas, definidas
entre las coordenadas cartesianas y las esféricas, definidas por las relaciones:
Estas relaciones se hacen singulares cuando tratan de extenderse al propio eje 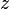 , donde
, donde  , en el
, en el
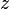 , donde
, donde  , en el
, en el cual φ, no está definida. Además, φ no es continua en ningún punto 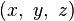 tal que
tal que 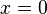 .
.
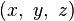 tal que
tal que 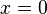 .
.La función inversa 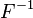 entre los dos mismos abiertos puede escribirse en términos de las relaciones inversas:
entre los dos mismos abiertos puede escribirse en términos de las relaciones inversas:
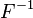 entre los dos mismos abiertos puede escribirse en términos de las relaciones inversas:
entre los dos mismos abiertos puede escribirse en términos de las relaciones inversas:
Relación con las coordenadas cilíndricas
y sus inversas
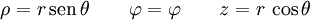
- fuente:wikipedia
Movimiento retrogrado

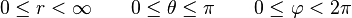
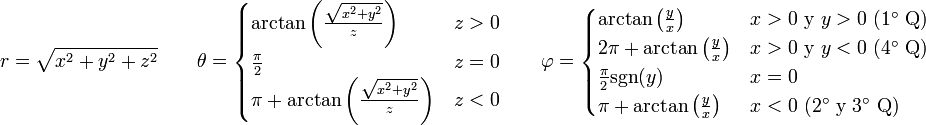
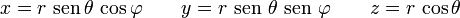
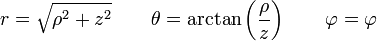


No hay comentarios:
Publicar un comentario