La transendencia de π y la cuadratura del círculo.

Siendo el área del círculo y el área del cuadrado, donde y 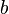son el radio del círculo y el lado del cuadrado respectivamente, se observa que, para el cuadrado de área igual a la del círculo, 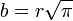. En otras palabras, el radio del círculo y el lado del cuadrado son proporcionales, siendo 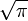el factor de proporción.

Esto implica que, si fuera posible cuadrar el círculo, se podría obtener 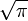con regla y compás, es decir, se lograría obtener 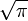por medio de operaciones algebraicas. Sin embargo, los números trascendentes son un subconjunto de los números reales que se caracterizan, entre otras cosas, precisamente por no ser obtenibles a partir de tales operaciones. Si 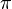es un número trascendente, como demostró Lindemann, 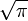también lo es. De aquí la imposibilidad de cuadrar el círculo a la manera griega.

fuente: wikipedia